TRE Oct 1945 home page

T. R. E. JOURNAL
ISSUED BY THE
TELECOMMUNICATIONS RESEARCH ESTABLISHMENT
MALVERN
October 1945

DELTA OBOE
By A.M. Uttley B.Sc., Ph.D.

When Oboe bombing accuracy was being examined it became clear that the pilot's inability to fly accurately down a beam caused important errors; at the same time ideas were growing that in any control system involving a human operator one should display to him what he should do rather than some picture of the situation. If one displays a picture of the situation the operator must work out by deduction or by trial and error what to do; this mental problem is entirely eliminated if one displays directly "what to do". As a result training is shorter and accuracy higher. For the Oboe case it is easier to fly in a given direction than along a given line, and an improvement in bombing should result if the pilot were told the direction to fly rather than his distance right or left of the beam. We may divide the problem into three sections dealing with the display, the operator, and the control system.

The Display

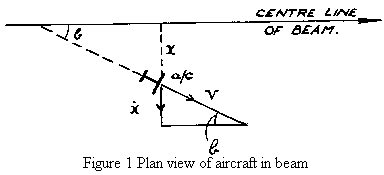
Fig. 1, shows an aircraft flying the neighbourhood of a beam.
x = Distance of aircraft to right of beam.
V = Ground speed of aircraft.
b = Inclination of track of aircraft to the beam.

PLEASE NOTE:
Due to the difficulty of showing mathematical symbols on a web page, the scans of the original pages are used here.

The velocity triangle shows that

S = k (x + k'ẋ) ..........................(3)

and the pilot be asked to make S = 0.       (3) is called a "Display Equation"; k is a measure of the modulation per unit distance from the centre of the beam.

If at any instant x = xo, ẋ = ẋo, and S = So and if xo + k'ẋc = o where ẋo is the correct rate for that instant, then we may write

So = k (xo + k'ẋo) or So = kk' (ẋo - ẋc) .............................(4)

so that S is a linear measure of the error in ẋ or b of the pilot's track, again assuming b to be small.

Figure 2. Delta Approach

Suppose the pilot succeeds in -always keeping S = o then at any instant were he to fly in a straight line (see Fig.2) he would reach the beam in a time x/-ẋ i.e. k' secs., Since his velocity inwards is -ẋ; we conclude that at all times the pilot is aiming at a point on the beam k' secs. ahead; this is the Delta Oboe Display system.

The Operator
The pilot cannot quickly change b or x to make S = o. We will make two assumptions about the pilot's behaviour.

I. The pilot will endeavour to bank the aircraft through an angle ψ equal to -k"S so that his rate of change of direction will be proportional to his error in direction and tending to reduce it. (See Equation 4).

II. It has been shown that an operator tends to make a control movement proportional to an error display, but with a fairly constant time lag T due to the finite duration of physiological and psychological processes. In this case to achieve (I) the pilot will move the ailerons through an angle z proportional to the difference between actual bank and demanded bank.

The above assumptions result in an "Operator Equation",

z_t+T - B (ψ_t + k"S_t) ........................(5)

showing that aileron position at time t + T is proportional to bank error perceived at time t. The negative sign shows that the control movement is such as to reduce error, and the constant B is a psychological constant and may be regarded as a measure of the operator's sensitivity.

The Control System
Neglecting the effects of rate of turn and side slip upon rate of roll we may write

z = C (dψ/dt) .................................... (6)

when C contains aerodynamic constants and airspeed assumed constant.

It can also be shown that:‑

ẍ = g tan ψ ........................................................ (7)

for a turn in which height is not lost.

Combining (6) and (7) and assuming tan ψ= ψ, have the "Control Equation".

= (g/C) z ................................................(8)

The Overall Performance
We can now combine the Display equation (3), S = k(x+k'ẋ) the Operation Equation (5) z_t+T - B (ψ_t + k"S_t) and the Control equation (8) = (g/C) z to eliminate z and S, and obtain a performance equation involving x only.

We may expand the l.h.s. of (5) by Taylor's theorem and write

or in operational form

where p represents the differential operator d/dt.
Substituting from (7), (8) and (9), (5) may be rewritten:-

or (Cp³e^Tp + Bp²) x = g B k"S

or p²x = (-g k"S) / 1 +(C/B)p e^Tp ............................................(10)

Combining (10) and (3) we find that

This is the Performance Equation.

Case I

C = T = o. .............................(11) reduces to

{p² + g kk' k" p + g kk"} x = 0 ..........................................(12)

an oscillation whose natural (undamped) period = 2π/ω where ω² = gkk" and of one overshoot behaviour if the damping factor

Case II
C ≠ o, T = o a lag C/B is introduced, and it has been shown (i) that no serious instability is introduced if

To discover the significance of C/B we may combine equations (5) and (6) letting T = o and ρ = ψ - k"S

We find the cῤ = - Bρ or ρ = ρ_oe^-t/C/B .......................................................(l4)

In other words C/B is the time constant of banking and is in practice of the order of seconds; if B is small (see (1)) i.e. if the pilot makes a small aileron movement for a given bank error, the time constant is long. It has been suggested that in practice the pilot will subconsciously decrease B until (13) is disobeyed and oscillation commences; the pilot will then increase B until by trial and error he achieves a just stable state.

Case III C ≠ o, T ≠o.
T is actually of the order of tenths of seconds, an order smaller than C/B. We may commence to examine the case by letting e^Tp P = 1 + Tp; we see that a second lag has been introduced. It has been shown (ii) that no serious instability is introduced if ω((C/B) + T) < 0.4. It is therefore necessary for C/B or ω to be slightly smaller than in Case II, but to all intents and purposes T can be neglected in Delta Oboe.

Theoretical Conclusions
1. From (12) the period of oscillation depends on k the modulation gradient of the beam and k" the bank introduced by the pilot per unit signal.

2. From (12b) the stability depends on kt the rate-aiding time constant.

3. Fran (13) the natural period of oscillation must be greater than 15.7 times the banking time constant of man. and aircraft.

4. The personal reaction time T of the pilot has negligible effect upon the overall performance.

5. The overall performance would be more predictable if the rather indeterminate constant k" of the pilot's behaviour were prescribed in some way, This could be done by making

S = k (x + k' ẋ) + ψ/k" ....................................(15)

so that S would now be a measure of bank error instead of course error. The Operator-Equation (5) would then become

zt+T = -B k" St (16)

resulting in the same overall performance equation as before. It would then be possible to calculate k' accurately.

6: The banking time constant is also rather indeterminate depending as it does upon B the pilot's movement of the aileron per unit bank error, but variations in B do not have a very great effect upon the overall performance. B could be prescribed by making the display signal S a measure of error in aileron position. We would then have a display equation

S = k (x + k' ẋ) + ψ/k" + ψ/Bk"

and an operator equation S = o with the same overall performance as before. Step (5) is being tried out. Steps (5) and (6) are both necessary when using Oboe to control an autopilot.

Practical Results
1. An untrained operator flew an Oboe trainer using a link aircraft, both with and without Delta. The results are shown in Fig.3.

2. 24 operational pilots trained on Normal Oboe flew the same trainer. The pilot's weaving with Delta Oboe was reduced to 2/5 of its value with Normal Oboe. A typical result is shown in Fig.4.

3. Bombing trials showed that the pilot's Weaving with Delta Oboe was reduced to 2/5 of its value with Normal Oboe.